Notes on the reconstruction of Pereire's Arithmetical machine 1750 / Stephan Weiss 2008

[ …]

Exerpt of the register of the Royal Academy of Sciences, 5th of May 1751

We have examined on the orders of the Academy an Arithmetical machine, presented by Mr. Pereire, of whom the Company has already approved the method of teaching speech to mutes.
Mr. Pereire cites in the paper he read to the Academy on the 16th of last December, everything currently known about machines of this kind, among which those by Mrs. Pascal, Perrault, Lépine and Boistissandeau are the best-known. The first and two last take up a somewhat embarrassing volume and consist of many wheels, springs, ratchets and other parts which make them costly, subject to repair, and inconvenient in use.
The rabdological abacus of Mr. Perrault is much simpler, and it is this instrument that the machine of Mr. Pereire resembles most. The abacus is composed of small rulers, each containing two columns of numbers, one on top of the other, separated by an empty space.The numbers in the first column are along the order 0,1,2,3 etc until 9 and those in the second column are in the reverse order, 9,8,7 etc.
until 0, and the operation is by shifting the rulers in the grooves that contain them. Once they arrive at the bottom end of their travel, a ratchet which is built into the body of the ruler finds an opening for engaging in a groove in the neighbouring ruler, making it advance by one step to mark tens of units for the first ruler, and if the ruler arrives at the bottom of its travel and thus indicates no number in the bottom window, one makes the ruler move up until the pointer that is moving it stops at the top of its groove - thus one finds at the bottom window the units that accompany the ten that the ratchet has been made to indicate, as will be explained more thoroughly in describing the use of this instrument .

Instead of putting the two columns on top of each other on each slide, Mr. Perrault could have put them side by side, in putting one slightly higher than the other, and placing the indicator windows in which the numbers appear conveniently accordingly. In this way the abacus would have no more need for such substantial length.
The machine of Mr. Pereire adopts this idea, but is more ingenious.
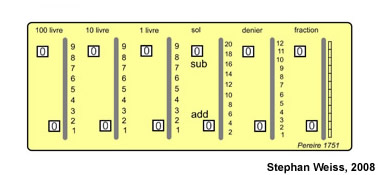
Instead of rulers, it uses small wooden wheels or very short cylinders, like trictrac stones, all put on a common axle. The cylindrical surfaces of these stones or wheels thus become rods without end: he has divided the circumreference of each of the wheels in thirty equal parts where he has written two series of numbers: the first contains three times the numbers 1 2 3 4 5 6 7 8 9 0, the second one three times the numbers 0 9 8 7 6 5 4 3 2 1. Of these wheels, there is one for the "Deniers", one for the "Sols", one for the simplest fractions like 1/2, 1/3, 1/4, 1/6, etc. and seven for the whole numbers, units, tens, hundreds, thousands, etc. until millions
: and all these wheels together form but one cylinder three inches long to 18 eights in diameter, enclosed in a small trunk-shaped box.
There are on top of this box as many grooves as there are wheels, each occupying one third of the circumreference of the cylinder, by which one makes the wheels turn with the tip of a stylus, in the same way one makes Mr. Perrault´s abacus´ rods move, taking the number one wants from 1 to 9 and 0, with this advantage that here the columns of numbers follow each other without interruption, one is never obliged to make the wheels turn back to make the number which results from the operation one makes, appear, as Perrault´s abacus often requires.
Mr. Pereire has divided the circumreference of the wheel into thirty parts as opposed to twenty, so that the slits which are on top of the box would occupy only one third of the circumreference of the circle, instead of half, which would not have been as convenient. He could have divided them in forty or fifty parts as well, and then the slits would have taken only 1/4th or 1/5th part of the circle cicumreference, but this larger number of divisions would have necessitated making the wheels larger.
Additionally, on top of the box which contains the wheels, there are two rows of windows along the length of the box, one on the front, and one on the back, those here to find the sum or the product of the numbers one wishes to add or multiply, those there to dial the number from which one wants to subtract , or which one wants to divide by another. The means which Mr. Pereire has found to advance a wheel every time the preceding one passes 10 is very ingenious. For this, along one of the flat sides of each wheel he has made thirty teeth representing more or less the teeth of a cog wheel. The other face is reserved to place a small balance, made hooked on one side, and along an inclined plane on the other. Each time ten divisions of this wheel have passed, the inclined plane meets a tooth fixed on the iron plate between the two wheels. This tooth forces the balance to move into the body of the wheel, thus pushing out the hook of which the other side consists, through the iron plate, which has an opening especially for this purpose, hooking behind one of the thirty teeth on the flat side of the neighbouring wheel, and making it advance one step. This step made, the inclined plane now being past the tooth on the iron plate, is tilted back into its place by means of a spring, the hook thus returns into the body of the wheel and retracts from the neighbouring wheel after having made it move by the value of one tooth.
This entire arrangement seems well-thought-out to us, simple and convenient, and we judge it to be worthy of the approval and inclusion in the array of machines approved by the academy.
This all having been said, there are only two things left which we believe would be good to draw the attention of our readers to :

1. By means of the arithmetic machine by Mr. Pereire, one can do without the help of pen and paper, the four arithmetic operations, the first two in pounds, shillings and pences, and the seven kinds of fractions. This last peculiarity of the machine by Mr. Pereire, which is also unique about it, is all the more useful as one can add or subtract fractions of different denominators with the same ease as if operating on whole numbers : one will find for example that 1/4 1/3 3/8 5/24 makes1 1/16 and when 5/12 is subtracted, 3/4 remain.

2. That the machine of Mr. Pereire, of which the volume is indicated above, should not be of considerable price, but nevertheless that those willing to procure the machine should advertise Mr. Pereire, as the price could even be lower as the number procured is larger. It is of little surprise that the mechanical arts will be happy to have this new machine, which by itself is very suitable for raising interest, and which is very useful not only for mute children, but for all those wishing to learn the science of numbers.

Mr. Pereire resides Quai des Augustins, in the Hôtel d´Auvergne.

[…]

Le journal des Sçavans, 1751,  pages 507-511

** Translation by Cris Stenella, 2008 **

Valéry Monnier
www.ami19.org
www.arithmometre.org
2008